Phương pháp giải phương trình chứa ẩn dưới dấu căn bậc hai-Kỹ thuật sử dụng đạo hàm

Phương pháp giải phương trình chứa ẩn dưới dấu căn bậc hai

Kỹ thuật sử dụng đạo hàm

Phương pháp

Quy tắc 1.

Nếu $y=f(x)$ có đạo hàm cấp 1: $y’=f'(x)>0;\forall x\in D$ thì hàm số đồng biến trên D và đồ thị cắt 0x tại một điểm duy nhất $x={{x}_{0}}$.

Suy ra: phương trình: $f(x)=0$ có nghiệm duy nhất $x={{x}_{0}}$.

Nếu $y=f(x)$ có đạo hàm cấp 1: $y’=f'(x)<0;\forall x\in D$ thì hàm số nghịch biến trên D và đồ thị cắt 0x tại một điểm duy nhất $x={{x}_{0}}$.

Suy ra: Phương trình: $f(x)=0$ có nghiệm duy nhất $x={{x}_{0}}$.

Quy tắc 2.

Nếu $y=f(u)$ có đạo hàm cấp 1: $y’=f'(u)>0;\forall x\in D$ và $y=g(v)$ có đạo hàm cấp 1: $y’=g'(v)<0;\forall x\in D$ thì đồ thị $y=f(u)$ và $y=g(v)$ cắt nhau tại một điểm duy nhất $u=v$.

Suy ra: phương trình: $f(u)=g(v)$ có nghiệm duy nhất $u=v$.

Quy tắc 3.

Nếu $y=f(t)$ có đạo hàm cấp 1: $y’=f'(t)>0;\forall x\in D$ thì $f(u)=f(v)\Leftrightarrow u=v$.

Suy ra: Phương trình: $f(u)=f(v)$ có nghiệm khi và chỉ khi $u=v$.

Các bước thực hiện

Tìm tập xác định của phương trình.
Biến đổi phương trình về dạng:$f(x)=0$ hoặc $f(u)=f(v)$ hoặc $f(u)=g(v)$.
Tính đạo hàm $f’\left( x \right);g'(x)$, rồi dựa vào tính đồng biến-nghịch biến của hàm số (quy tắc) để kết luận nghiệm của phương trình.

Ví dụ minh họa

Ví dụ 1

Giải các phương trình sau: $\sqrt[3]{2x+1}+\sqrt[3]{2x+2}+\sqrt[3]{2x+3}=0$ (1).

Giải

Tập xác định: D = R.

Đặt $f(x)=\sqrt[3]{2x+1}+\sqrt[3]{2x+2}+\sqrt[3]{2x+3}=0$

Ta có:

$\begin{array}{l}
f'(x) = \frac{2}{{\sqrt[3]{{{{\left( {2x + 1} \right)}^2}}}}} + \frac{2}{{\sqrt[3]{{{{\left( {2x + 2} \right)}^2}}}}} + \frac{2}{{\sqrt[3]{{{{\left( {2x + 3} \right)}^2}}}}} > 0\\
\forall x \ne \left\{ { – \frac{1}{2}; – 1; – \frac{3}{2}} \right\}
\end{array}$

Suy ra hàm số f(x) đồng biến trên tập:

$T=\left( -\infty ;-\frac{1}{2} \right)\cup \left( -\frac{1}{2};-1 \right)\cup \left( -1;-\frac{3}{2} \right)\cup \left( -\frac{3}{2};+\infty \right)$

Ta có: $f\left( -\frac{1}{2} \right)=3;f\left( -1 \right)=0;f\left( -\frac{3}{2} \right)=-3$

Ta có bảng biến thiên của hàm số f(x):

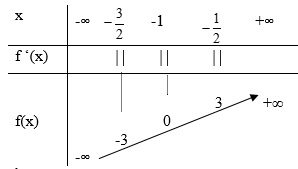
Từ bảng biến thiên ta thấy f(x) = 0 <=> x = -1.

Vậy phương trình đã cho có duy nhất một nghiệm x = -1.

Ví dụ 2

Giải phương trình: $\sqrt {3x + 1} + \sqrt {x + \sqrt {7x + 1} } = 4$

Giải

Điều kiện: $D=\left[ \frac{7-\sqrt{57}}{2};+\infty \right)$

Xét hàm số $f(x)=\sqrt{3x+1}+\sqrt{x+\sqrt{7x+2}}$

Ta có f(x) là hàm liên tục trên D và:

$f’=\frac{3}{2\sqrt{3x+1}}+\frac{1+\frac{7}{2.\sqrt{7x+2}}}{2\sqrt{x+\sqrt{7x+2}}}>0,\forall x\in D$.

Suy ra: hàm số f(x) luôn đồng biến trên D.

Mặt khác, ta thấy f(1)=4 và:

Nếu x >1 suy ra f(x)>f(1) nên pt vô nghiệm.

Nếu x<1 suy ra f(x)<f(1) nên pt vô nghiệm.

Vậy x=1 là nghiệm duy nhất của phương trình đã cho.

Ví dụ 3

Giải phương trình sau: $\sqrt[3]{x+2}+\sqrt[3]{x+1}=\sqrt[3]{2{{x}^{2}}+1}+\sqrt[3]{2{{x}^{2}}}$

Giải

Đặt: $u=\sqrt[3]{x+1};v=\sqrt[3]{2{{x}^{3}}}$ thì phương trình đã cho trở thành:

$\begin{align}
& \sqrt[3]{{{u}^{3}}+1}+u=\sqrt[3]{{{v}^{3}}+1}+v \\
& \Leftrightarrow f(u)=f(v) \\
\end{align}$

Xét: $f(t)=\sqrt[3]{{{t}^{3}}+1}+t$ là một hàm liên tục và có :

$f'(t)=\frac{{{t}^{2}}}{\sqrt[3]{{{({{t}^{3}}+1)}^{2}}}}+1>0$

nên f(t) luôn đồng biến.

Do đó:$f(u)=f(v)\Leftrightarrow u=v\Leftrightarrow 2{{x}^{2}}=x+1\Leftrightarrow x=1,x=-\frac{1}{2}$

Vậy phương trình có nghiệm x=1, x=-1/2.

————————-

Download tài liệu:

PDF: tại đây.

Word: Tại đây.

————————–

Xem thêm:

———————-

User

Phương pháp giải phương trình chứa ẩn dưới dấu căn bậc hai-Kỹ thuật sử dụng đạo hàm

Đăng bởi ADMIN vào 17/12/201917/12/2019